# ground stations (GSs), ground vehicles (GVs), unmanned aerial vehicles (UAVs)
Algorithm Overview
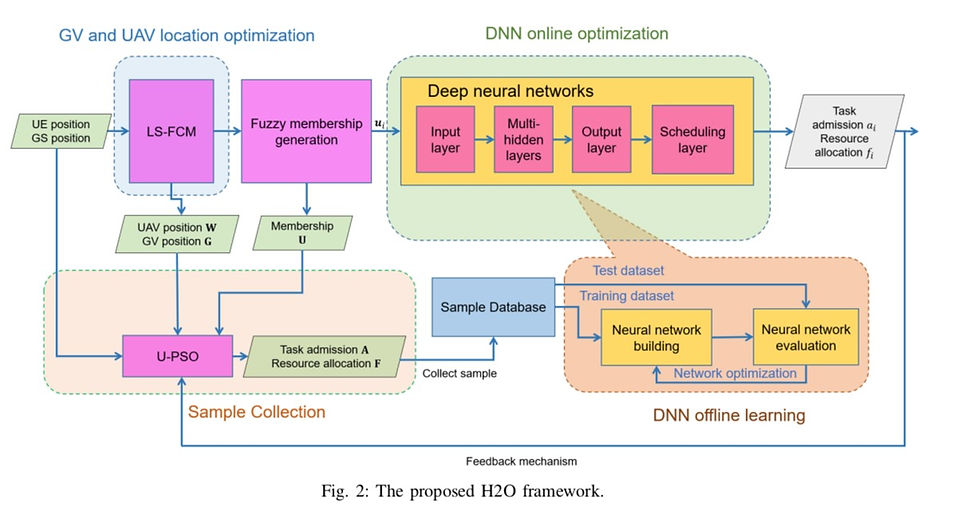
In this section, we provide a novel algorithm named hybrid
deep learning-based online offloading (H2O) to solve Problem
P 1. The structure of the H2O algorithm is illustrated in
Fig. 2, which is composed of four parts: GV and UAV
location optimization, sample collection, DNN offline learning
and DNN online decision. The main procedure of the H2O algorithm is divided into the offline training phase and the
online optimization phase.
The offline training phase is carried out in the remote cloud
server with high computational and storage capabilities. We
regard the optimization problem P 1 as the mapping function
from the input system parameters to the output resource allocation solutions.
We use a DDN to fit this mapping function. To
this end, we must find the resource allocation solution under
specific system parameters. In other words, we require samples
to train the DNN. To this end, we provide one algorithm to
solve Problem P 1 to obtain the training samples
In specific,
we first adopt the LS-FCM algorithm in Subsection-B to obtain
the locations of the UAVs and GVs. We then deploy the UAVs
and GVs according to the calculated locations. Then, we pro-
pose a novel U-PSO algorithm in Subsection-C to obtain the
offloading selection
and resource allocation solution based on
the novel fuzzy membership information that can capture the
small-scale channel information and the relative interference
among the UEs.
Finally, a supervised learning algorithm is used
to train the DNN that can be applied to scenarios where
the number of UEs is varying.
Then, the trained DNN can be implemented for online
calculation. In particular, each UE only needs to input its
membership values (detailed in Subsection-C), then the DNN can
output its offloading choice and computing resource allocation
result.
This has much lower computational complexity since
it only needs to perform some simple algebraic calculations
instead of solving the original optimization problem through
high-complexity heuristic algorithms.
In addition, during the
online implementation, some results output by the DNN will
be regarded as new samples and stored in the database in
the cloud. These samples will be used for offline training and
to update the DNN. This is very important since it can track
the variations of real scenarios.
Algorithm 1 LS-FCM algorithm
Input: GS positions, UE positions, ε, c, τ , T F CM .
Output: C.
1: Initialize the locations of cluster centers. Calculate μ ij
according to Eq. (22).
2: Fix some centers of C according to the GS positions.
3: ∆G(1) = 1, G(0) = 0, t = 1.
4: while |∆G(t)| > ε and t < T F CM do
5: Calculate the remaining cluster centers of matrix C
using Eq. (21).
6: Calculate the objective function G(t) using Eq. (20).
7: Update each μ ij using Eq. (22).
8: ∆G(t) = G(t) − G(t − 1).
9: t = t + 1.
10: end while
Comments